Matematiksel Düşünme Becerisi Yazıları – IX

Matematiksel Düşünme Becerisi ve Çözünürlük Ontolojisi (Prof. Dr. Aslan GÜLCÜ & Berrak BAŞAK)

-Varlığın Matematiksel Katmanlarında Özet Bir Yolculuk-

Dijital Çağda Varlığı Yeniden Düşünmek

Matematiksel düşünme becerisinin bir yüzü de sadece sayılar ve formüllerle sınırlı olmayan, gerçekliğin katmanlarını sistematik olarak çözümleme tarafına dönüktür. Bu denemede, dijital çağın bize sunduğu “çözünürlük” kavramını ontolojik bir araç olarak kullanarak, varlığın temellerini matematiksel düşünme perspektifinden inceleyeceğiz. Tıpkı bir dijital görüntünün pikselleri nasıl daha yüksek çözünürlükle daha ayrıntılı görünür hale geliyorsa, varlığın da farklı çözünürlük seviyelerinde farklı gerçeklik katmanlarının açığa çıkmasını değerlendireceğiz.

Çözünürlük Metaforu: Dijitalden Ontolojiye

Dijital özelinde modern teknolojinin bize kazandırdığı temel kavramlardan biri de “çözünürlük” (resolution) kavramıdır. Çözünürlük, en basit ifadeyle bir nesneyi ne kadar ayrıntılı görebildiğimizi belirten kavramdır. Günümüzde bu kavram günlük yaşamımızın parçası haline geldi öyle ki telefonumuzun kamerasından televizyonumuzun ekranına kadar her yerde çözünürlük değerleri ile karşılaşmaktayız. Düşük çözünürlükte bulanık görünen bir fotoğraf karesi, yüksek çözünürlükte keskin ayrıntılar kazanır. Ancak çözünürlük sadece teknolojik bir terim değildir; aynı zamanda gerçekliği algılama biçimimizi de tanımlar. Gözümüzle gördüğümüz dünya belirli bir çözünürlük seviyeleri ile sınırlıdır, ancak mikroskoplar, teleskoplar, dürbünleri kameralar ve diğer görüntüleme araçları bu sınırları aşarak daha önce görüp bilemediğimiz (mikroda ayrıntıları, makroda büyüklükleri) ortaya çıkarmaya devam etmektedir. Bu yeni durum, varlığın farklı katmanlarının ancak farklı çözünürlük seviyelerinde görülebileceğini iddia etmekte ve bizi ontolojik bir soruyla karşı karşıya bırakmaktadır: Gerçek nedir? Gerçek hangi çözünürlüktedir? Gerçek hangi çözünürlük seviyesinde en doğru şekilde kendini gösterir? Sorular devam eder…

Bir dijital görüntüde 72 DPI’dan 300 DPI’ya çıktığımızda, aynı varlığın çok daha ayrıntılı katmanlarını müşahede edebiliriz. Bu teknolojik metaforu ontolojiye uyarlarsak, varlığın farklı “çözünürlük seviyelerinde” nasıl farklı varlık katmanları açığa çıkardığını gözlemleyebiliriz.

Bu yazıda ele alınan yaklaşımın orijinalliği, geleneksel ontolojinin statik kategorilerini dinamik bir matematiksel model içinde yeniden düşünülmesini sağlamaktır. Varlık, artık sabit kategoriler değil, sürekli değişen ve gelişen çözünürlük fonksiyonları olarak ele alınma konumuna gelmeye başlamıştır.

Çözünürlük Katmanlarında Varlığın Anatomisi

Gündelik yaşamımızdan basit bir örnek alalım: Masa örtüsü. Normal gözle baktığımızda, masa örtüsünün ipliklerden dokunmuş düz ya da desenli bir varlık olarak görürüz. Aynı anda çözünürlüğü arttırarak ve matematiksel düşünme becerisi ile çalışırsak aşağıdaki yeni katmanları gözlemleyebiliriz:

Matematiksel Düşünme Süreci:

1. Soyutlama: Masa örtüsünü geometrik bir yüzey olarak modelleyebiliriz.
2. Ölçek Analizi: Gözlem mesafemizi tanımlarız ve çözünürlük fonksiyonu kurarız.
3. Diferansiyel Yaklaşım: Çözünürlüğü artırmak için limit kavramını kullanırız.
4. Fraktal Geometri: Her katmanın bir önceki katmanın alt-yapısı olduğunu matematiksel olarak şöyle ifade edebiliriz.

Bu matematiksel çerçeveye sadık kalarak çözünürlük katmanlarını da matematiksel işlemlerle gözlemlemiş oluruz ki bu süreç de aşağıdaki şekilde çalışır:

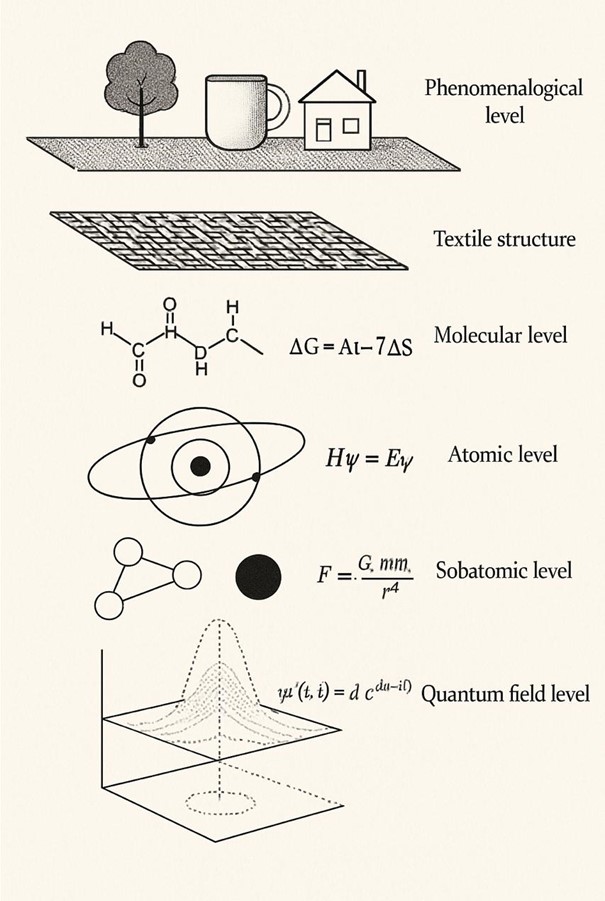
1. Makro Seviye (R₁): Fenomenolojik Varlık
2. Mezo Seviye (R₂): Tekstil Yapısı
3. Mikro Seviye (R₃): Moleküler Düzen
4. Nano Seviye (R₄): Atomik Gerçeklik
5. Atom Altı Seviye (R₅): Kuantum Varlığı
6. Kuantum Alan Seviyesi (R₆): Foton Etkileşimleri

Matematiksel Düşünme Becerisi’nin Rolü:

Bu süreçte matematiksel düşünme becerisi şu şekilde devreye girer:

• Modelleme: Her katman için uygun matematiksel yapı seçimi
• Soyutlama: Fiziksel gerçekliği matematiksel simgelere dönüştürme
• Analiz: Karmaşık yapıları basit bileşenlere ayırma
• Sentez: Farklı katmanlar arasında matematiksel köprüler kurma
• Limit Düşüncesi: Sonsuz küçüğe ve büyüğe gitme yetisi
• Fonksiyonel İlişkiler: Değişkenler arası matematiksel bağımlılıkları görme

Matematiksel düşünme becerisinin bu örnekle beraber bir slogan değil, aktif olarak kullanılabilecek kognitif araçlar haline geldiği/geleceği de görülmektedir.

Matematiksel Düşünme Becerisi ve Ontolojik Geçişler

Yukarıda sıralanan her çözünürlük seviyesi ve aralarındaki geçişler, matematiksel düşünme becerisi gerektiren karmaşık işlemlerdir. Bu geçişler, sadece ölçek değişimi değil, aynı zamanda kavramsal paradigma değişimlerini de gösteren kavramsal kategorilerdir.

Ontolojik Çözünürlük Teorisi

Bu çalışmanın orijinal yanı, “Ontolojik Çözünürlük Teorisi” adını verdiğimiz yaklaşımdır. Bu teori, şu temel ilkeler üzerine kuruludur:

1. Varlık Süreklilik İlkesi: Varlık, ayrık kategoriler değil, sürekli çözünürlük spektrumudur. (Not: Kanımca aslında varlık kategorileri ayrık ama sürekli yapılardadır. Dünyamızda kullanılan matematiğin süreklilik/yoğunluk ilkesinden dolayı şimdilik böyle ifade edilmesi gerekmektedir. Ayrık (discrete) temelli bir matematik inşa edilmesi halinde varlık kategorilerinin ayrık olduğu görülecektir.)
2. Matematiksel Katmanlılık: Her çözünürlük seviyesi, kendi matematiksel dilini gerektirir.
3. Gözlemci Bağımlılığı: Çözünürlük, gözlemcinin matematiksel araç setine bağlıdır.
4. Ontolojik Tamamlayıcılık: Ontolojik tamamlayıcılık, bir varlığın belirli bir boyutundaki çözünürlüğünü arttırdığımızda, diğer boyutlardaki netliğinin azalması durumudur. Tıpkı Heisenberg’in belirsizlik prensibi gibi: “Bir parçacığın konumunu tam ölçtüğümüzde hızındaki belirsizliğin artması durumu.”

Örneğin masa örtüsünü atom seviyesinde incelediğimizde (yüksek fiziksel çözünürlük), onun “masa örtüsü” olarak anlamsal bütünlüğü kaybolur. Artık sadece karbon, hidrojen vd. atomlarını görürüz, yani “masa örtüsü” kavramı bulanıklaşır.  Tam tersi de geçerlidir: Masa örtüsünü estetik bir nesne olarak kavradığınızda (yüksek anlamsal çözünürlük), atomik yapısı görünmez hale gelir. Hülasa varlığın farklı boyutlarını (fiziksel, kimyasal, estetik, işlevsel) aynı anda maksimum netlikle göremezsiniz. Bir boyuttaki odaklanma, diğer boyutlarda “bulanıklık” oluşturur. Bu, ontolojik bir sınırlılıktır.

Dijital Teknoloji ve Ontolojik Keşif

Dijital teknolojiler, ontolojik keşiflerimizi genişletmeye yardımcı olabilir. Varlığı farklı çözünürlük seviyelerinde gözlemlememizi sağlayan elektron mikroskopu, atomik kuvvet mikroskobu, kuantum bilgisayarlar sadece araç olarak değil, aynı zamanda ontolojik kategorilerimizi şekillendiren katalizörlerdir. Özellikle Yapay Zekâ algoritmaları, veri setlerinde insanın göremediği ve düşünemediği çözünürlük seviyelerini açığa çıkarır. Derin öğrenme algoritmalarının çalıştırılması ile de varlığın gizli katmanlarını (hidden layers) matematik dili ile ifade edebilir seviyeye gelebiliriz.

Pratik Uygulamalar ve Sonuçlar

Bu ontolojik çözünürlük yaklaşımı, çeşitli disiplinlerde yeni perspektifler sunabilir:

• Bilim Felsefesi: Bilimsel teorilerin, farklı çözünürlük seviyelerindeki varlık katmanlarının açıklaması.
• Matematik Eğitimi: Matematiksel kavramların, çözünürlük seviyelerine göre kademelendirilmesi.
• Teknoloji Felsefesi: Dijital teknolojilerin ontolojik etkisinin sistematik olarak incelenmesi gibi.

Diğer yandan bu yaklaşımın sınırları ve sınırlılıkları da söz konusudur. Çözünürlük metaforu, haliyle varlığın tüm boyutlarını kapsamamaktadır. Özellikle bilinç, anlam, ahlak, erdem ve değer gibi kavramlar, çözünürlük arttırımı ile açıklanamayabilir.

Varlığın Matematiksel Şifresi mi?

Matematiksel düşünme becerisi, varlığın kodlarını çözmek için kullanılan evrensel bir dildir. Çözünürlük kavramı da bu dilin dijital çağdaki yeni ifade biçimidir. Masa örtüsünden fotona kadar uzanan bu yolculuk, varlığın tek bir şey olmadığını, aksine çok katmanlı matematiksel yapılar olduğunu gösterir. Bu örnek, matematiksel düşünme becerisinin sadece hesaplama değil, varlığın çok boyutlu doğasını keşfetme aracı olduğunu gösterir. Her çözünürlük seviyesi farklı matematik dalları gerektirir ve her geçiş, ontolojik bir sıçrama yaratır. Bu ontolojik çözünürlük yaklaşımı, geleneksel felsefenin statik kategorilerini dinamik matematiksel modeller ile değiştirerek, varlığı anlamada yeni ufuklar açabilir. Dijital çağın bu şekilde bize sunduğu teknolojik imkânlar, sadece varlığı gözlemlememizi değil, aynı zamanda varlığı kavramamızı ve dönüştürmemiz gerektiği düşüncesi taşımaktadır. Buradan hareketle şunu söylemek artık daha kolay hale gelmektedir: “Gelecekte hayatımıza girecek yüksek hızlı/kapasiteli kuantum bilgisayarlar ve yapay zekâ teknolojileri, varlığın daha da derin çözünürlük seviyelerini açığa çıkaracak ve ontolojik anlayışımızı köklü biçimde değiştirip dönüştürecektir.” İşin bizi en çok ilgilendiren yanı ise bu değişimin matematiksel düşünme becerisinin rehberliğinde gerçekleşecek olmasıdır.